Long sequence capabilities enable a variety of applications like summarizing long form documents, such as contracts or other legal documents, or answering questions on those documents. A longer context also means more guiding examples can be provided leading to potentially higher accuracy. However, training a long sequence model is expensive because the attention mechanism’s computation scales quadratically with sequence length. Instead of training from scratch, the LLM community has proposed a variety of positional interpolation methods [2] [5] [6] to extend the maximum sequence length of existing open source models. This blogpost discusses considerations when applying such techniques to ALiBi, a particular type of LLM positional encoding popularized by the BLOOM [11] and MPT [12] model families. In particular, we discuss:
- Positional Extrapolation versus Positional Interpolation without fine tuning
- TL;DR – interpolation appears better than extrapolation for ALiBi embeddings
- Precision and its impact on ALiBi
- TL;DR – extending ALiBi embeddings to long sequences should be done in FP32 precision
Interpolating ALiBi
Attention with Linear Biases (ALiBi) [1] is a type of positional encoding, a method in Transformers (the core module of LLMs) for imparting positional information to the hidden states of each token. Some other common positional encoding methods include absolute positional encoding (original Transformer [13], GPT-2 [14]) and Rotary Position Embedding (RoPE) (RoFormer [3], Llama [15], Llama 2 [7]).
The original ALiBi paper states that ALiBi outperforms RoPE when extrapolating to sequences beyond what the model has seen during training. However, recent literature [2] [5] [6] has popularized positional interpolation (PI) as a method that significantly strengthens RoPE-based models’ long sequence capabilities. We provide Figure 1 from [2] to illustrate the differences between positional extrapolation and interpolation on RoPE.
Figure 1: Positional Extrapolation VS Interpolation
(from Figure 1, page 2 of [2])
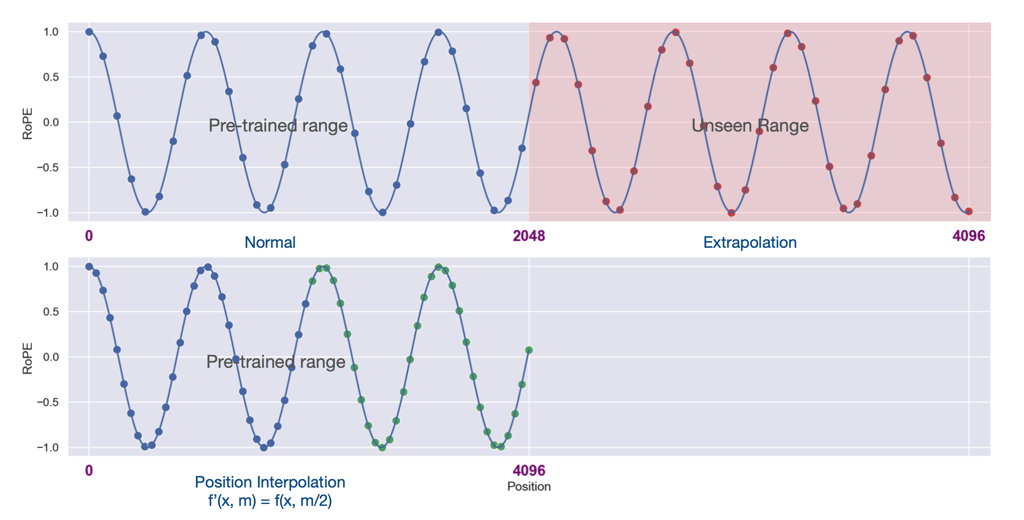
The original PI paper focuses mainly on RoPE, and does not perform any experiments on ALiBi-based models. As such, we experiment with applying PI to ALiBi and observing the resultant perplexity. We note that, unlike the original authors in [2], we do so without additional model training.
Figure 2: BLOOM 7B perplexity per sequence position
(lower is better)
In the above plot, we show the per-token perplexity of BLOOM-7B [11] when applied to sequences of length 7168. These perplexities are averaged across 1000 sequences taken from mC4-3.1.0 [17], filtered by language for those that appear in ROOTS [18], the original training dataset of BLOOM-7B. It’s clear that interpolating ALiBi, in this limited scenario, allows the model to maintain reasonable perplexity per token, even without any finetuning!
However, perplexity can be an opaque metric; to make this performance gap more concrete, we evaluated BLOOM-7B on SCROLLS [16], a widely used collection of long-sequence benchmarks, again without any finetuning. We extend the maximum sequence length to 8192 and compare extrapolation against interpolation.
Table 1: BLOOM 7B on SCROLLS
(for all metrics, higher is better)
| Task | Metric | Extrapolation | Interpolation |
| NarrativeQA | f1 | 1.6313 | 4.1731 |
| Qasper | f1 | 11.2172 | 21.3295 |
| QMSum | rouge1 | 0.8612 | 7.2892 |
| rouge2 | 0.0202 | 1.1162 | |
| rougeL | 0.7971 | 6.7557 | |
| SummScreenFD | rouge1 | 4.0185 | 6.4948 |
| rouge2 | 0.0309 | 0.7504 | |
| rougeL | 3.8773 | 5.7613 | |
| GovReport | rouge1 | 10.1860 | 18.3927 |
| rouge2 | 1.1405 | 4.0023 | |
| rougeL | 8.8337 | 15.0320 | |
| Contract NLI | acc | 0.13 | 0.06 |
| acc_norm | 0.12 | 0.06 | |
| em | 12.0 | 6.00 | |
| QuALITY | acc | 0.17 | 0.26 |
| acc_norm | 0.29 | 0.33 | |
| em | 29.0 | 33.0 |
We can see that, on most long sequence tasks (with the exception of Contract NLI), interpolating to 8192 allows the model to perform much better than extrapolating.
ALiBi and Precision
The experiments above were run in full precision (FP32). However, often we’ll try to reduce precision to FP16 or BF16 for faster inference.
FLOAT16
When extrapolating BLOOM 7B in FP16 to sequence length 8192, we noticed some heads of ALiBi had problematic values. Consider the following code snippet, taken from the build_alibi_tensor function of modeling_bloom.py in the transformers repository:

Right before the return statement, the alibi variable has shape (batch_size x num_heads x seq_length). Let’s examine the last few values of the first head when we use a sequence length of 8192:

This is all well and good; as described in the paper, each sequence position in the attention matrix gets a unique value added to it. However, when we convert this tensor to FP16, something interesting happens:

It turns out that in FP16, these last 20 positions end up being mapped to only 5 different values, such that every 3-4 positions all get the same positional encoding! This is due to FP16 having a lower numerical precision than FP32. In fact, when we plot out the last 192 positions of this attention head, the “linear” embeddings of ALiBi turn out to be not so linear in FP16:
Figure 3: ALiBi Head 0 of 32 in [8000,8192)
BFLOAT16
Another data type for accelerated training is BFloat16 [19]. When we try out this dtype instead, we observe the following:
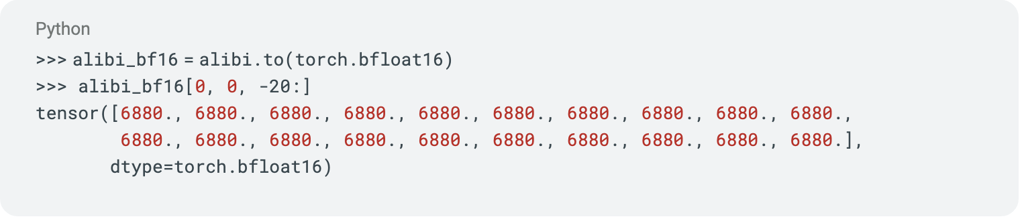
Even worse, now the last 20 positions all get the same positional embedding.
When we compare the allocation of the 16 bits in BF16 and in FP16, we see why BF16 has reduced precision: it allocates 3 fewer bits to the significand than FP16. Adding BF16 to our previous plot highlights the extent of this lower precision, especially in the later positions of the sequence.
Figure 4: ALiBi Head 0 of 32 in [8000,8192), 3 precisions
The following table summarizes the effect of these lower precision data types by comparing different ranges of sequence positions and their resulting number of unique embeddings in attention head 0 (out of 32 total) for each data type:
Table 2: ALiBi buckets for Different Precision Levels
| FP32 | FP16 | BF16 | |
| 0-999 | 1000 | 1000 | 491 |
| 1000-1999 | 1000 | 876 | 129 |
| 2000-2999 | 1000 | 604 | 77 |
| 3000-3999 | 1000 | 421 | 53 |
| 4000-4999 | 1000 | 394 | 50 |
| 5000-5999 | 1000 | 211 | 28 |
| 6000-6999 | 1000 | 211 | 27 |
| 7000-7999 | 1000 | 211 | 27 |
| 8000-8192 | 192 | 41 | 6 |
From the above, it’s clear that with increasing sequence length, lower precision makes it harder to distinguish ALiBi positional embeddings.
DIFFERENT ALIBI HEADS
Recall that ALiBi embeddings have a head-specific slope m=2-8(i+1)/n, where n is the number of attention heads and i is the attention head index in the range [0,n) (Section 3 page 5 of [1]). Since different attention heads will have different slopes and, naturally, different ranges for the embedding values, one might ask whether different attention heads might be affected differently by precision. Let’s recreate Figure 4, but for some of the other 31 attention heads:
Figure 5: Different ALiBi heads on the range [8000,8192)
The plots in Figure 5 all look pretty similar to Figure 4! If we convert the above plot into table format (see Table 3 below), we can see that the number of buckets for the range 8000-8192 really doesn’t change much across head indices. So it seems, at least in this particular configuration, all attention heads are equally affected by this precision issue.
Table 3: Unique values per attention head in the range 8000-8192
| FP32 | FP16 | BF16 | |
| Head 0 | 192 | 41 | 6 |
| Head 9 | 192 | 35 | 5 |
| Head 19 | 192 | 49 | 7 |
| Head 31 | 192 | 49 | 7 |
Interpolation and Precision
When we look at the values in Table 2, we notice that this discrepancy between data types isn’t really noticeable in the first 1000 positions. Indeed, if we recreate Figure 4 for the range [0,1000), we can see that FP32, FP16 and BF16 perfectly match:
Figure 6: ALiBi Head 0 of 32 in [0,1000)
Can we mitigate the effects of quantization by scaling down all the embeddings to fit in this range instead? When we multiplied our ALiBi embeddings by 0.25 (as done when interpolating for 8192 sequence positions within a 2048 range), we found the following:

It turns out, if we recalculate Table 2 above with positional interpolation from 2048 to 8192, we get the exact same number of buckets for each precision level. So positional interpolation doesn’t mitigate this issue.
MITIGATING QUANTIZATION ISSUES WITH MIXED PRECISION
Internally, these observations have motivated development of better support for FP32 operations, such that all SambaNova models going forward are trained with a better range of mixed precision options. Look forward to future blog posts and releases featuring mixed precision!
Conclusion
In summary, we’ve presented two interesting findings related to LLMs that use ALiBi:
- Interpolating ALiBi to longer sequences outperforms extrapolation without additional training.
- ALiBi may require representation in a higher precision data type (or at least, a data type that allocates more bits to the significand) in order to preserve distinctive position embeddings for all sequence positions. This occurs regardless of whether we are extrapolating or interpolating ALiBi to longer sequences.
These are preliminary observations, and we advise further experimentation before adopting specific practices based on these results. Notably, the impact of positional encoding precision on downstream accuracy has not yet been evaluated. However, it is our hope that these findings will serve as a foundation for future research and experimentation. We remain committed to deepening our understanding of this topic to inform best practices in training and inference for long sequence models.
References
[1] Press, Ofir, Noah A. Smith, and Mike Lewis. “Train short, test long: Attention with linear biases enables input length extrapolation.” arXiv preprint arXiv:2108.12409 (2021).
[2] Chen, Shouyuan, et al. “Extending context window of large language models via positional interpolation.” arXiv preprint arXiv:2306.15595 (2023).
[3] Su, Jianlin, et al. “Roformer: Enhanced transformer with rotary position embedding.” arXiv preprint arXiv:2104.09864 (2021).
[4] Peng, Bowen, et al. “Yarn: Efficient context window extension of large language models.” arXiv preprint arXiv:2309.00071 (2023).
[5] bloc97. NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation., 2023. URL https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_ scaled_rope_allows_llama_models_to_have/.
[6] emozilla. Dynamically Scaled RoPE further increases performance of long context LLaMA with zero fine-tuning, 2023. URL https://www.reddit.com/r/LocalLLaMA/comments/ 14mrgpr/dynamically_scaled_rope_further_increases/.
[7] Touvron, Hugo, et al. “Llama 2: Open foundation and fine-tuned chat models.” arXiv preprint arXiv:2307.09288 (2023).
[8] Jiang, Albert Q., et al. “Mistral 7B.” arXiv preprint arXiv:2310.06825 (2023).
[9] Almazrouei, Ebtesam, et al. “The Falcon Series of Open Language Models.” arXiv preprint arXiv:2311.16867 (2023).
[10] DeepSeek. “DeepSeek-Coder.” URL https://github.com/deepseek-ai/DeepSeek-Coder.
[11] Workshop, BigScience, et al. “Bloom: A 176b-parameter open-access multilingual language model.” arXiv preprint arXiv:2211.05100 (2022).
[12] MosaicML. “Introducing MPT-7B: A New Standard for Open-Source, Commercially Usable LLMs.” URL https://www.mosaicml.com/blog/mpt-7b.
[13] Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems 30 (2017).
[14] Radford, Alec, et al. “Language models are unsupervised multitask learners.” OpenAI blog 1.8 (2019): 9.
[15] Touvron, Hugo, et al. “Llama: Open and efficient foundation language models.” arXiv preprint arXiv:2302.13971 (2023).
[16] Shaham, Uri, et al. “Scrolls: Standardized comparison over long language sequences.” arXiv preprint arXiv:2201.03533 (2022).
[17] Chung, Hyung Won, et al. “Unimax: Fairer and more effective language sampling for large-scale multilingual pretraining.” arXiv preprint arXiv:2304.09151 (2023).
[18] Laurençon, Hugo, et al. “The bigscience roots corpus: A 1.6 tb composite multilingual dataset.” Advances in Neural Information Processing Systems 35 (2022): 31809-31826.
[19] Wang, Shibo, et al. “BFloat16: The secret to high performance on Cloud TPUs.” URL https://cloud.google.com/blog/products/ai-machine-learning/bfloat16-the-secret-to-high-performance-on-cloud-tpus
[20] Jouppi, Norm. “Google supercharges machine learning tasks with TPU custom chip.” URL https://cloud.google.com/blog/products/ai-machine-learning/google-supercharges-machine-learning-tasks-with-custom-chip
